Khế Iêm
CẤT BƯỚC VÀO ĐỜI
Cuộc đời có những chuyện lạ lùng, không ai ngờ trước, chỉ với một chiếc máy điện toán đã đưa tới sự khám phá ra lý thuyết hỗn mang và hình học Fractal (Fractal Geometry), để rồi khoa học bước ra khỏi thế giới thuần lý, trừu tượng, trở về hiện thực, giải thích những hiện tượng đời sống. Lý thuyết hỗn mang được định nghĩa như sự vận hành ngẫu nhiên xảy ra trong một hệ thống tất định. Một sự cố xảy ra, xảy ra ai cũng có thể biết trước vì nó đã từng xảy ra trong quá khứ. Newton và Einstein đều căn cứ trên nguyên lý tất định như thế qua những công trình khoa học của họ. Nhưng thực tế không bao giờ có chuyện đó, vì chỉ một ảnh hưởng tình cờ rất nhỏ, ngoài sự hiểu biết của chúng ta, và có khi chẳng liên quan tới biến cố, cũng đưa tới kết quả khác hẳn.
Hơn hai ngàn năm kể từ Euclid, và gần ba trăm năm kể từ Newton, khoa học làm một cuộc cách mạng chưa từng có, với lý thuyết hỗn mang và hình học Fractal, trở thành Tân khoa học (New Science), thay đổi sự am hiểu toàn triệt của con người về hiện thực. Nếu khoa học được coi như triết học tự nhiên (Natural Philosophy) thì từ bấy lâu nay, đã không đúng với thực tại, bởi thế giới chúng ta đang sống không có những góc cạnh trơn tru (smooth edge), mà là thô nhám (rough edge). Những bề mặt trơn tru không có trong thiên nhiên, và hình học Euclid với đường thẳng, đường tròn, hình vuông, khối vuông, chỉ là những hình dạng lý tưởng của con người, không phải do thiên nhiên tạo ra. Euclid là một nhà toán học Hy lạp, sống vào khoảng 300 trước công nguyên, học trò của học trò Plato, là giáo sư và học giả tại Alexandria, Ai cập, tác giả cuốn “The Elements”. Định đề Euclid gồm 5 định đề căn bản:
1. Có thể vẽ một đường thẳng đi qua bất cứ hai điểm nào.
2. Có thể kéo dài đường thẳng đến vô tận.
3. Có thể vẽ một đường tròn với một bán kính và tâm điểm.
4. Tất cả các góc giống nhau đều bằng nhau.
5. Với một đường thẳng và một điểm ở ngoài đường thẳng, chỉ có thể vẽ một đường thẳng song song, và chỉ một đường thẳng mà thôi.
Hình học Euclid còn gọi là hình học phẳng, được coi như bản thánh kinh về toán học, chi phối và được áp dụng cho đến nửa thế kỷ thứ 19, khi hình học phi Euclid (Non-Euclid), được phát hiện với những nhà toán học như Carl Friedrich Gauss (1777-1855), Nhà toán học Nga Nikolay Ivanovich Lobachevsky (1793-1856) và nhà toán học Hungary Janos Bolyai (1802-1860). Hình học phi Euclid chỉ không đồng ý với hình học Euclid một điểm: “Với một đường thẳng L và từ một điểm ngoài đường thẳng, có thể vẽ vô số những đường thẳng song song với đường thẳng L.” Tới thế kỷ thứ 15, Johannes Kepler (1571-1603) là người đầu tiên nhận ra quĩ đạo của những hành tinh là hình bầu dục (ellipse), không phải vòng tròn. Sir Issac Newton (1642-1727) và Gottfried Wilheim Leibniz (1646-1716) phát hiện ra Calculus, dùng phép vi phân (differentiation) và tích phân (integration), mở ra cách cửa vô cùng tận để diễn đạt và giải thích những bí ẩn của vũ trụ qua toán học. Và sau này Einstein dựa vào ý niệm của cả hình học phi Euclid và Newton để phát triển thuyết tương đối.
Vào thập niên 1970, Benoit Mandelbrot (sinh năm 1924), nhà toán học và vật lý Pháp sinh tại Ba lan, làm việc cho hãng IBM, đã khám phá ra hình học Fractal (Fractal Geometry), tác phẩm của ông, “The Fractal Geometry of Nature” (1977), khi quan sát và nghiên cứu những hình dạng không đều đặn, không liên tục và đứt gãy, trong thiên nhiên. Yếu tố chính của hình học Fractal là sự tự tương đồng (Self- Similarity), có nghĩa là nếu phóng đại một hình ảnh, nó sẽ giống y hình ảnh chưa phóng đại. Cụ thể, khi bổ một nhánh bông cải (cauliflower), cứ bổ nhỏ dần, nhỏ dần, miếng nhỏ trông giống y miếng lớn và toàn thể. Mandelbrot khởi đầu là một nhà kinh tế học. Những nhà kinh tế tin tưởng rằng một thay đổi rất nhỏ sẽ không có ảnh hưởng gì trong thời kỳ dài, nhưng Mandelbrot nhìn vào hệ thống một cách toàn thể, không loại bỏ những thay đổi nhỏ ra khỏi cái toàn cảnh lớn, chú ý đến sự thăng trầm trong những dữ kiện khác nhau, nhận ra đặc điểm, giá bông gòn trở lại sau nhiều năm. Khi nhìn vào dữ kiện từ nhiều thang số khác nhau, những dạng thức tái diễn trở lại, như khi vẽ biểu đồ về sự thay đổi giá cả hàng ngày và hàng tháng, biểu đồ trông rất quen thuộc. Một lần ông giải quyết tiếng ồn, lúc mất tiếng, lúc bất thình lình lại bùng lên, trong đường dây điện thoại dùng để nối với nhiều computer. Những dạng thức tiếng ồn luôn luôn xảy ra từng chùm, và khi lấy một thời kỳ tiếng ồn, phóng đại lên, ông thấy có vài thời kỳ không tiếng. Những thời kỳ tiếng ồn luôn luôn có thời kỳ, có tính truyền dẫn tốt ẩn ở bên trong.
Hình học Fractal giữ vai trò then chốt trong lý thuyết hỗn mang. Nếu hình học Fractal là sự tự tương đồng ở bất cứ thang số nào, giống như nhánh bông cải thì hỗn mang tùy thuộc vào sự nhạy cảm của những điều kiện khởi đầu và không thể đoán trước. James Gleick, trong cuốn “Chaos, Making a New Science” nhấn mạnh, trong thế kỷ 20 có ba cuộc cách mạng lớn về khoa học, đó là lý thuyết tương đối, lý thuyết cơ học lượng tử và lý thuyết hỗn mang. “Thuyết tương đối bác bỏ ảo tưởng Newton về sự tuyệt đối của không gian và thời gian, thuyết lượng tử bác bỏ giấc mơ Newton về tiến trình kiểm soát đo lường và thuyết hỗn mang bác bỏ sự không tưởng của Laplace về sự tiên đoán tất định.” Pierre-Simon Laplace (1749-1827) là một nhà vật lý Pháp, nổi tiếng trong một trích dẫn, thường gọi là “Laplace’s Demon”, cho rằng trạng thái hiện tại của vũ trụ là kết quả của quá khứ và nguyên nhân của tương lai. Mọi thứ đều được tiên đoán trước, không tình cờ, không chọn lựa, chắc chắn, và quá khứ hoàn toàn quyết định tương lai, theo nguyên lý tất định.
Nhưng từ Newton đến Poincaré, không ai giải quyết nổi tình trạng nan giải và đơn giản về quĩ đạo của mặt đất (earth) và hai mặt trời (sun). Và phải đợi lý thuyết hỗn mang và hình học Fractal mới giải tỏa được bế tắc rất nhỏ này, sai một ly đi một dặm, đã đẩy khoa học theo một chiều tuyến tính gần ba thế kỷ. Tuy nhiên, Tân khoa học không phủ nhận, mà bao gồm cả khoa học cổ điển. Cũng như hình học Fractal là nối dài, không thay thế mà chỉ làm phong phú và sâu xa thêm sức mạnh của hình học Euclid. Phi tất định bao gồm tất định, phi tuyến tính bao gồm tuyến tính, cũng như hỗn mang bao gồm những yếu tố trật tự.
Vấn đề ba thiên thể (Three-body problem)
Khi Newton khám phá ra luật chuyển động và trọng lực (Laws of Motion and Gravitation), ông dùng hai khám phá này để giải thích quĩ đạo trái đất chung quanh mặt trời – mặt trời là một định tinh trong không gian và quĩ đạo trái đất là hình bầu dục. Có thể nói, mặt trời là một attractor của trái đất. Nhưng vũ trụ không phải chỉ có trái đất và mặt trời mà còn nhiều thiên thể khác, như vậy quĩ đạo của toàn thể vũ trụ đâu phải chỉ là một hình bầu dục. Đến đầu thế kỷ 20, nhà toán học Henri Poincaré (1854-1912) trong một nghiên cứu về vấn đề ba thiên thể (Three-body Problem) cho thấy, sự tiến hóa của hệ thống như vậy thường hỗn mang, bởi một xáo trộn nhỏ trong trạng thái đầu tiên của một trong ba thiên thể có thể thay đổi triệt để trạng thái sau cùng. Sự thay đổi nhẹ nhàng đó khó có thể phát hiện bằng phương tiện đo lường, vì thế không thể nào đoán trước chuyện gì sẽ xảy ra. Lý do vì, trọng lực là một lực phi tuyến tính, và trong hệ thống ba thiên thể, mỗi thiên thể tạo ra lực trên hai thiên thể kia, dẫn tới sự phản hồi phi tuyến tính và chuyển động hỗn mang của những quĩ đạo. Poincaré chính là người đầu tiên khám phá ra hỗn mang, và sự sai lầm của chủ nghĩa tất định, nhưng không ai quan tâm tới sau nhiều thập niên, bởi những nhà khoa học còn bận tậm tới hai lý thuyết quan trọng là thuyết lượng tử và thuyết tương đối.
Vào thập niên 1960, bằng computer, những nhà khoa học nhìn ra quĩ đạo trái đất và hai mặt trời theo mô hình như sau:
Hình 1
So sánh hai hình bên trái và phải, với một điểm trái đất ở giữa hai mặt trời: trái đất chạy thẳng từ dưới lên trên, vòng qua mặt trời ở bên phải, rồi chạy tới vị trí cũ, tạo thành hai quĩ đạo gần giống nhau, sau đó bắt đầu phân kỳ, không bao giờ lập lại như thế nữa. Sự phân kỳ này là do những khác biệt rất nhỏ mà chúng ta gọi là sự tùy thuộc mẫn cảm vào những điều kiện ban đầu (Sensitive Dependence on Initial Conditions). Hai hình trên chỉ là quĩ đạo trong một khoảng thời gian rất ngắn.
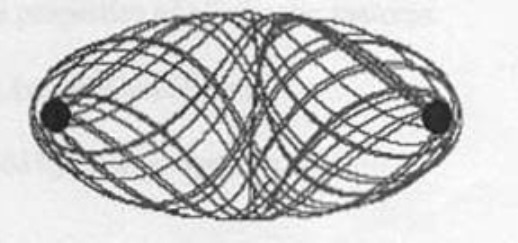
Hình 2
Đây là toàn quĩ đạo của trái đất và hai mặt trời, trong tiến trình tới vô hạn. Quĩ đại trái đất sẽ không bao giờ tự nó lập lại, tuy hỗn mang ở bên trong nhưng vẫn nằm trong một cấu trúc, luôn luôn thăng bằng và ổn định. Hệ thống trọng lực đơn giản này là một hệ thống hỗn mang.
Hiệu ứng cánh bướm (Butterfly Effect)
Lý thuyết hỗn mang được nhà khí tượng học Edward Lorenz (sinh năm 1927) khám phá ra vào năm 1961, khi ông dùng computer, viết một chương trình căn bản toán học để nghiên cứu mô hình đơn giản của thời tiết – sự tương quan giữa ba yếu tố khí tượng phi tuyến tính: nhiệt độ, áp xuất và sức gió – làm sao một luồng không khí nổi lên rồi tan đi dưới sức nóng mặt trời. Những mã số computer của Lorenz gồm 12 phương trình toán học cho những luồng chảy của không khí, diễn đạt sự liên hệ giữa nhiệt độ và áp suất, giữa áp suất và sức gió. Vì mã số computer tất định, ông nghĩ rằng khi đưa vào cùng một giá trị ban đầu, sẽ có kết quả y như vậy khi chạy chương trình. Ông ngạc nhiên khi nhận được kết quả khác biệt, kiểm lại thì ra, ông đã đưa vào từng lúc những sai biệt rất nhỏ.
Câu chuyện được kể lại như sau:
Vào một ngày năm 1961, Lorenz muốn thấy một đoạn đặc biệt nào đó một lần nữa. Thay vì chạy cả một chuỗi dài vì rất lâu, ông đi tắt, bắt đầu ở khoảng giữa thay vì từ đầu. Ông đánh thẳng con số đã in ra từ lần trước rồi bỏ đi uống cà phê. Khi trở lại khoảng một giờ sau, ông không tin ở mắt mình, biểu đồ mới tiến triển khác hẳn với biểu đồ lúc đầu. Thay vì hai dạng thức giống nhau, nó phân kỳ và kết thúc hoàn toàn khác. Sau đó ông mới biết có sự lầm lẫn, thay vì đánh đúng con số là 0.506127 (trong bộ nhớ computer), ông lại chỉ đánh 0.506. Sự sai biệt một phần năm ngàn, thật không hợp lý, và ông nghiệm ra, sự khác biệt rất nhỏ trong những điều kiện đầu, như một hơi gió thoảng, cũng có thể tạo nên tai biến. Tiên đoán thời tiết trở nên không thể được trong một thời gian lâu dài vì chỉ cần sự thay đổi tí ti của sức gió, áp xuất hay nhiệt độ, ngay cả những yếu tố ngoài thời tiết cũng làm xáo trộn khí hậu như một cánh bướm đập chẳng hạn.
Biểu đồ sau đây cho thấy sự phân kỳ của hai dạng thức 0.506 và 0.506127, chỉ khác biệt một sai số rất nhỏ là 0.000127. Đoạn đầu thì trùng lặp, nhưng sau đó thì phân kỳ rất lớn. (Hình 3)
Hình 3
Với mục đích thử nghiệm, ông nghiên cứu thêm sự đối lưu của chất lỏng (fluid convection), gọi là hệ thống dạng khí (gaseous system), bỏ chất khí (homogenous, preferably elemental, gaseous substance) vào một chiếc hộp hình chữ nhật và đun nóng lên.
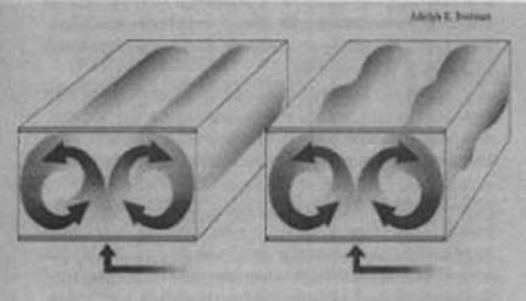
Hình 4
Mới đầu, một phần chất lỏng gần với vách hộp bắt đầu nóng và nổi lên, tới một độ nóng nhất định, chất lỏng cuộn lại, nằm theo chiều dài hộp (hình bên trái). Chất lỏng ấm nổi lên về một bên, đồng qui, chất lỏng nguội rơi vào bên khác – tiến trình đối lưu. Với nhiệt độ bình thường, sự chuyển động tròn của chất lỏng sẽ bình thường và biết trước. Nhưng khi nhiệt độ nóng hơn (hình bên phải), hệ thống mất ổn định, chao đảo dọc theo chiều dài hình ống viên tru (cylinder)ï, từ sau ra trước. Những dòng cuộn không đơn giản cuộn lại trong cùng một chiều, mà cuộn lại theo một chiều, ngừng một lát rồi cuộn nghịch lại. Sau đó, đột nhiên, chất lỏng cuộn nghịch lại lần nữa, dao động tiếp tục ở một thời điểm và tốc độ không thể biết trước. Với nhiệt độ cao, hệ thống trở nên hỗn mang.
Sau đó ông làm thử nghiệm với hệ thống quay nước (waterwheel), cũng cho kết quả tương tự.
Bạn đọc có thể đọc như một ghi chú (trong bài).
Thí nghiệm với hệ thống dạng khí, chúng ta có ba phương trình vi phân phi tuyến tính, biểu diễn trên hai trục hoành độ (thời gian t) và tung độ x, y, z. Ba biểu đồ x, y, z lần lượt như sau:
Với X là độ quay của hình ống viên trụ, trị số 10 (delta) là độ trơn của chất lỏng. Chúng ta có phương trình:
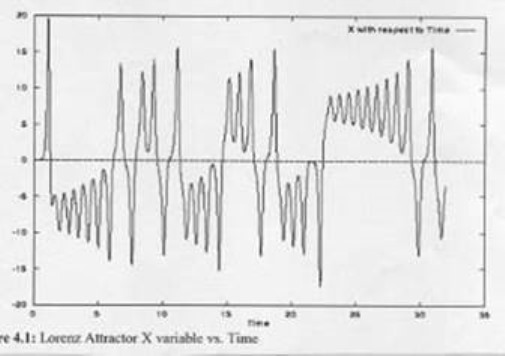
dx/dt = -10x + 10y
Hình 5
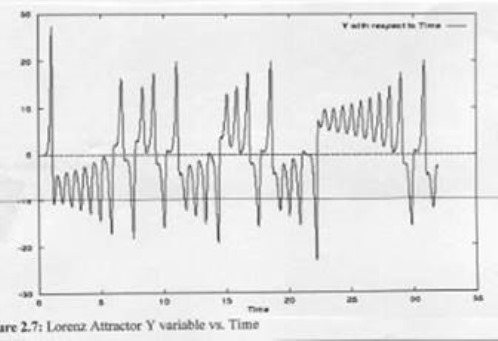
Với Y là sự khác biệt nhiệt độ giữa hai bên đối diện của hình ống viên trụ, trị số 28 (r) là sự khác biệt nhiệt độ của chất lỏng ở trên mặt và phần dưới đáy. Chúng ta có phương trình:
dy/dt = 28x – y +xz
Hình 6
Với Z là độ lệch của hệ thống theo tuyến tính, trị số 8/3 (b) là tỉ lệ giữa bề rộng và bề cao
của hộp. Chúng ta có phương trình:
dz/dt = -8/3x + xy
Hình 7
Nếu kết hợp biến số (variable) của ba phương trình trên một không gian (vị tướng) nhiều chiều (phase space), chúng ta có hiệu ứng cánh bướm. Gọi như thế vì những quĩ đạo luôn luôn phản hồi và lập lại, nhưng vì những điều kiện đầu không bao giờ giống nhau, nên dù lập lại nhưng các quĩ đạo không bao giờ trùng lặp. Đây là biểu đồ nhìn qua một mặt phẳng:
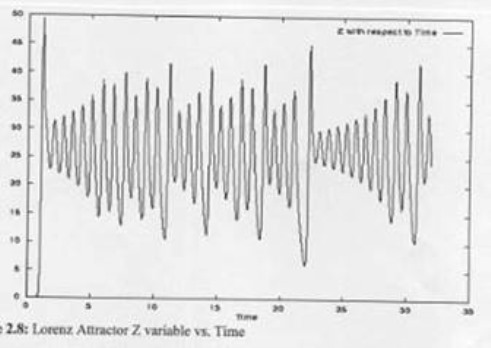
Hình 8
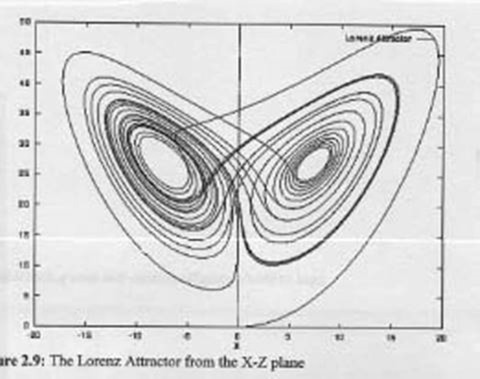
Nhìn hình vẽ trên, giống như hai cánh bướm (có khi là hình dạng hai mắt cú, có khi giống như hai chiếc đĩa giấy, nằm song song), nối kết với nhau bởi một cuộn dây chỉ, được vẽ từ một điểm ở ngoài cánh bướm, vòng qua cánh bên phải, vươn tới trung tâm cánh bên trái, và tiếp tục đan dệt qua lại giữa hai cánh, chuyển động tưởng như ngẫu nhiên, phản ảnh tiến trình hỗn mang. Hiệu ứng cánh bướm Lorenz theo đúng với tiến trình quĩ đạo của ba thiên thể, tùy thuộc mẫn cảm vào những điều kiện đầu tiên, những thay đổi rất nhỏ trong một hệ thống đồng qui có thể tạo nên kết quả khác biệt rất lớn. Và hình sau đây giúp chúng ta nhìn thấy rõ hơn quĩ đạo của ba phương trình trên computer, trên một không gian đa chiều, rất dễ hình dung.
Hình 9
Nhận ra được hiệu ứng cánh bướm của Lorenz, chúng ta nhận ra được sự vận hành của hiện tượng hỗn mang. Dĩ nhiên mỗi hiện tượng có một hiệu ứng cánh bướm khác nhau, những yếu tố trật tự vì thế là yếu tính của trật tự. Để hiểu được yếu tố trật tự (hay dạng thức) hiện ra như thế nào, cần tới sự giải thích của phương trình vận thức (Logistic Equation).
Bản đồ vận thức (The Logistic Map)
Nhà kinh tế chính trị học người Anh, Thomas Malthus (1766-1834), quan tâm tới điều kiện sinh sống ở Anh vào thế kỷ 19, nhận xét rằng dân số tăng theo cấp số nhân trong khi thực phẩm chỉ tăng một cách tuyến tính, và như thế sẽ đưa tới nạn đói tập thể, nếu không điều hòa sự sinh sản, nhất là nơi những giai cấp thấp. Nhưng trên thực tế, khi dân số tăng tới một mức nào đó, sẽ không tăng nữa. Thập niên 1940, nhà toán học Áo Pierre Francois Verhulst (1804-49), đưa ra một phương trình qua đó có thể tìm ra được tình trạng ổn định trong việc tăng dân số. Phương trình vận thức phi tuyến tính của Verhulst – đã bị bỏ quên, có lẽ vì thiếu dữ kiện dân số thích đáng để áp dụng – tiên đoán, trong những trường hợp phù hợp, dân số sẽ cân bằng và ổn định. Nếu dân số giảm dưới một mức nhất định nào đó, năm sau có khuynh hướng tăng, trong khi lên quá cao (thiếu chỗ ở và lương thực), sẽ giảm xuống.
Vào thập niên 1970, Robert May (sinh năm 1936), một nhà sinh thái học đã vén màn bí mật, khi chú ý tới phương trình Verhulst, cho rằng gia tăng sự mẫn cảm của hệ thống, tạo nên sự dao động (oscillation) kỳ lạ, dân số tăng quá nhiều trong năm sẽ có sự bù trừ, giảm trong năm kế tiếp, và trở lại tăng trong năm sau nữa. Dạng thức lập lại cứ trong 2 năm, và lập lại mãi mãi, gọi là sự trùng lặp (iteration).
Phần này cũng chỉ như một ghi chú, chứng minh một cách chính xác những yếu tố trật tự hiện ra như thế nào.
X (next) = rx(1-x)
Công thức phi tuyến tính trên có ý nghĩa, nếu X trở nên lớn hơn, thì (1 – X) sẽ trở nên nhỏ hơn, tạo nên sự phản hồi (feedback)
Thí dụ với sự tăng giảm cá.
X tiêu biểu cho một số giữa Zero và 1. Zero tiêu biểu cho sự tuyệt giống và 1 tiêu biểu cho sự tăng trưởng tối đa dân số. r là mức độ tăng (growth rate), một hằng số.
Cho r = 2.6
Giả thử x = 0.2.
1-x = 0.8 và x(x-1) = 0.2 x 0.8 = 0.16
Nhân với 2.6 và chúng ta có 0.416.
Lấy đầu ra là 0.416 làm đầu vào, bắt đầu lại với công thức trên. Bây giờ chúng ta bắt đầu
với x = 0.416 và được 0.6317. Số cá tăng.
Bắt đầu với 0.6317 và được 0.6049. Số cá giảm.
Bắt đầu với 0.6049 và được 0.6214. Số cá lại tăng.
Rồi tiếp tục chúng ta được: 0.6117, 0.6176, 0.6141, 0.6162, 0.6150, 0.6156, 0.6152,
0.6155, 0.6153, 0.6154, 0.6153, 0.6154, 0.6154, 0.6154.
Với r = 2.6 chúng ta chỉ có một giá trị ổn định là 0.6154 (negative feedback)
Làm như thế với r = 3.1, cuối cùng chúng ta có những số 0.5582, 0.7645, 0.5582, 0.7645.
Với r = 3.1 chúng ta có hai giá trị ổn định: 0.5582 và 0.7645.
Làm như thế với r = 3.5, cuối cùng chúng ta có được: 0.8750, 0.3828, 0.8270, 0.5011,
0.8750, 0.3828, 0.8270.
Với r = 3.5 chúng ta có 4 giá trị ổn định: 0.8750, 0.3828, 0.8270, 0.5011
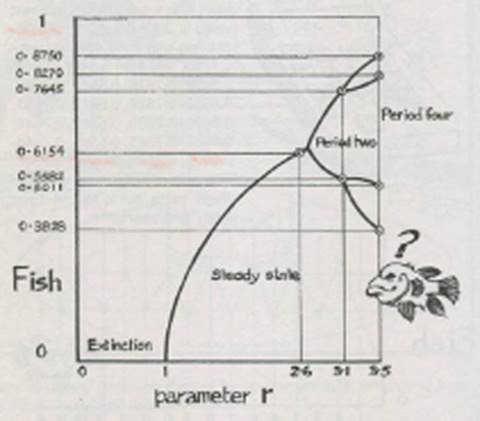
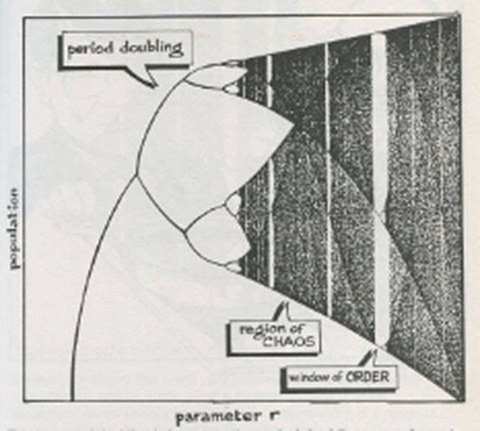
Theo cách tính trên, nếu lấy đầu ra (output) của một lần tính, làm đầu vào (input) của một lần tính thứ hai, và cứ như thế mãi mãi, cho ta ý niệm về sự trùng lặp những con số ổn định. Có nghĩa là trong một hệ thống hỗn mang, những dạng thức trật tự xuất hiện, nhưng luôn luôn thay đổi và không bao giờ giống với dạng thức trật tự ban đầu. Điểm rẽ (Birfurcation Point) đầu tiên khi r = 2.6 (trên trục hoành độ), tạo nên trị số ổn định 0.6154 (trên trục tung độ), nhưng sau đó sự mẫn cảm của hệ thống gia tăng, trị số ổn định bị dao động, và vẽ nên những đường quĩ đạo tiến tới thời kỳ hai, với r= 3.1 và hai trị số ổn định 0.5582 và 0.7645. Và ở thời kỳ 4, với r= 3.5 và bốn trị số ổn định là 0.8750, 0.3828, 0.8270, 0.5011, rồi sau đó đi vào hỗn mang. Nhưng trong hỗn mang luôn luôn tiếp tục xuất hiện những yếu tố ổn định, và lập lại toàn cách tính, nếu chúng ta tiếp tục như thế mãi mãi, so sánh 2 hình dưới đây.
Hình 10
Hình 11
Chúng ta vừa ra khỏi khu rừng khoa học chằng chịt, nhìn lên bầu trời xanh trong, thoảng thoát, tưởng như đã bỏ lại đằng sau một đoạn đường đời, dài thăm thẳm, và cảm thấy lòng thanh thản. Khoa học, rốt cùng cũng chỉ là sản phẩm của nhận thức và trí tuệ con người, và thơ hay văn học nghệ thuật là một mặt khác nữa, đã từng song hành làm nên nền văn minh. Nếu chủ nghĩa Hậu cấu trúc (Post-Structuralism) vào thập niên 1960 đã phá vỡ ranh giới giữa triết học và các ngành nghệ thuật, thì lý thuyết hỗn mang, một lần nữa phá vỡ bức tường kiên cố cuối cùng phân biệt giữa khoa học, triết học, văn học và đời sống, để bước vào cái toàn nhất. Cái toàn nhất ấy có khác nào vũ trụ hay bộ óc con người với hàng tỉ tế bào thần kinh không ngừng tương tác lẫn nhau, ngay cả trong giấc ngủ, là một bộ máy bí mật chưa ai có thể khám phá, bao gồm thế giới ý niệm là chiều tuyến tính và cảm xúc, tình tự con người là chiều phi tuyến tính, kết hợp làm thành cuộc đời. Bước vào cái toàn nhất là tự mình buông rơi trong hỗn mang, hòa tan mọi thế giới trong ta – nhưng biểu đồ quĩ đạo của ba thiên thể và hiệu ứng cánh bướm, những yếu tố trật tự vẫn cứ hiển hiện, bám riết không ngừng trong tâm trí, như vị thiền sư, sau khi trải qua biết bao nẻo đường gian nan, đi tìm chân lý, dừng lại trước cánh cửa cuối cùng, trầm ngâm, không biết làm sao khai mở. Những biểu đồ giống như công án thiền, những hấp lực kỳ lạ, phải được kiến giải, và như thế hãy cứ để những hình ảnh ám ảnh cho đến bao giờ tràn đầy, tức nước, đẩy chúng ta đi tới…